Javascript required
Skip to content Skip to sidebar Skip to footer
Home / Find a General Solution in Terms of Bessel Functions

Find a General Solution in Terms of Bessel Functions


Bessel Function of the First Kind

DOWNLOAD Mathematica Notebook EXPLORE THIS TOPIC IN the MathWorld Classroom

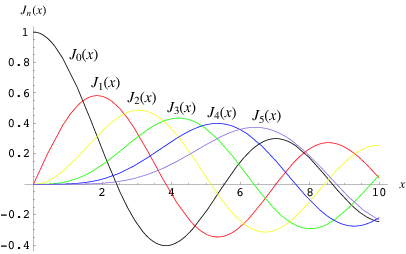
BesselJ

The Bessel functions of the first kind J_n(x) are defined as the solutions to the Bessel differential equation

x^2(d^2y)/(dx^2)+x(dy)/(dx)+(x^2-n^2)y=0

(1)

which are nonsingular at the origin. They are sometimes also called cylinder functions or cylindrical harmonics. The above plot shows J_n(x) for n=0, 1, 2, ..., 5. The notation J_(z,n) was first used by Hansen (1843) and subsequently by Schlömilch (1857) to denote what is now written J_n(2z) (Watson 1966, p. 14). However, Hansen's definition of the function itself in terms of the generating function

e^(z(t-1/t)/2)=sum_(n=-infty)^inftyt^nJ_n(z).

(2)

is the same as the modern one (Watson 1966, p. 14). Bessel used the notation I_k^h to denote what is now called the Bessel function of the first kind (Cajori 1993, vol. 2, p. 279).

The Bessel function J_n(z) can also be defined by the contour integral

J_n(z)=1/(2pii)∮e^((z/2)(t-1/t))t^(-n-1)dt,

(3)

where the contour encloses the origin and is traversed in a counterclockwise direction (Arfken 1985, p. 416).

The Bessel function of the first kind is implemented in the Wolfram Language as BesselJ[nu, z].

To solve the differential equation, apply Frobenius method using a series solution of the form

y=x^ksum_(n=0)^inftya_nx^n=sum_(n=0)^inftya_nx^(n+k).

(4)

Plugging into (1) yields

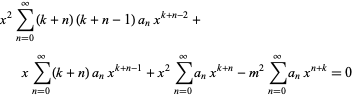x^2sum_(n=0)^infty(k+n)(k+n-1)a_nx^(k+n-2)+xsum_(n=0)^infty(k+n)a_nx^(k+n-1)+x^2sum_(n=0)^inftya_nx^(k+n)-m^2sum_(n=0)^inftya_nx^(n+k)=0

(5)

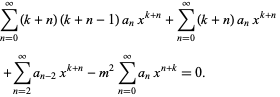sum_(n=0)^infty(k+n)(k+n-1)a_nx^(k+n)+sum_(n=0)^infty(k+n)a_nx^(k+n) +sum_(n=2)^inftya_(n-2)x^(k+n)-m^2sum_(n=0)^inftya_nx^(n+k)=0.

(6)

The indicial equation, obtained by setting n=0, is

a_0[k(k-1)+k-m^2]=a_0(k^2-m^2)=0.

(7)

Since a_0 is defined as the first nonzero term, k^2-m^2=0, so k=+/-m. Now, if k=m,

sum_(n=0)^infty[(m+n)(m+n-1)+(m+n)-m^2]a_nx^(m+n)+sum_(n=2)^inftya_(n-2)x^(m+n)=0

(8)

sum_(n=0)^infty[(m+n)^2-m^2]a_nx^(m+n)+sum_(n=2)^inftya_(n-2)x^(m+n)=0

(9)

sum_(n=0)^inftyn(2m+n)a_nx^(m+n)+sum_(n=2)^inftya_(n-2)x^(m+n)=0

(10)

a_1(2m+1)x^(m+1)+sum_(n=2)^infty[a_nn(2m+n)+a_(n-2)]x^(m+n)=0.

(11)

First, look at the special case m=-1/2, then (11) becomes

sum_(n=2)^infty[a_nn(n-1)+a_(n-2)]x^(m+n)=0,

(12)

so

a_n=-1/(n(n-1))a_(n-2).

(13)

Now let n=2l, where l=1, 2, ....

a_(2l) = -1/(2l(2l-1))a_(2l-2)

(14)

= ((-1)^l)/([2l(2l-1)][2(l-1)(2l-3)]...[2·1·1])a_0

(15)

= ((-1)^l)/(2^ll!(2l-1)!!)a_0,

(16)

which, using the identity 2^ll!(2l-1)!!=(2l)!, gives

a_(2l)=((-1)^l)/((2l)!)a_0.

(17)

Similarly, letting n=2l+1,

a_(2l+1)=-1/((2l+1)(2l))a_(2l-1)=((-1)^l)/([2l(2l+1)][2(l-1)(2l-1)]...[2·1·3][1])a_1,

(18)

which, using the identity 2^ll!(2l+1)!!=(2l+1)!, gives

a_(2l+1)=((-1)^l)/(2^ll!(2l+1)!!)a_1=((-1)^l)/((2l+1)!)a_1.

(19)

Plugging back into (◇) with k=m=-1/2 gives

y = x^(-1/2)sum_(n=0)^(infty)a_nx^n

(20)

= x^(-1/2)[sum_(n=1,3,5,...)^(infty)a_nx^n+sum_(n=0,2,4,...)^(infty)a_nx^n]

(21)

= x^(-1/2)[sum_(l=0)^(infty)a_(2l)x^(2l)+sum_(l=0)^(infty)a_(2l+1)x^(2l+1)]

(22)

= x^(-1/2)[a_0sum_(l=0)^(infty)((-1)^l)/((2l)!)x^(2l)+a_1sum_(l=0)^(infty)((-1)^l)/((2l+1)!)x^(2l+1)]

(23)

= x^(-1/2)(a_0cosx+a_1sinx).

(24)

The Bessel functions of order +/-1/2 are therefore defined as

so the general solution for m=+/-1/2 is

y=a_0^'J_(-1/2)(x)+a_1^'J_(1/2)(x).

(27)

Now, consider a general m!=-1/2. Equation (◇) requires

a_1(2m+1)=0

(28)

[a_nn(2m+n)+a_(n-2)]x^(m+n)=0

(29)

for n=2, 3, ..., so

for n=2, 3, .... Let n=2l+1, where l=1, 2, ..., then

where f(n,m) is the function of l and m obtained by iterating the recursion relationship down to a_1. Now let n=2l, where l=1, 2, ..., so

a_(2l) = -1/(2l(2m+2l))a_(2l-2)

(34)

= -1/(4l(m+l))a_(2l-2)

(35)

= ((-1)^l)/([4l(m+l)][4(l-1)(m+l-1)]...[4·(m+1)])a_0.

(36)

Plugging back into (◇),

y = sum_(n=0)^(infty)a_nx^(n+m)=sum_(n=1,3,5,...)^(infty)a_nx^(n+m)+sum_(n=0,2,4,...)^(infty)a_nx^(n+m)

(37)

= sum_(l=0)^(infty)a_(2l+1)x^(2l+m+1)+sum_(l=0)^(infty)a_(2l)x^(2l+m)

(38)

= a_0sum_(l=0)^(infty)((-1)^l)/([4l(m+l)][4(l-1)(m+l-1)]...[4(m+1)])x^(2l+m)

(39)

= a_0sum_(l=0)^(infty)([(-1)^lm(m-1)...1]x^(2l+m))/([4l(m+l)][4(l-1)(m+l-1)]...[4(m+1)m...1])

(40)

= a_0sum_(l=0)^(infty)((-1)^lm!)/(2^(2l)l!(m+l)!)x^(2l+m).

(41)

Now define

J_m(x)=sum_(l=0)^infty((-1)^l)/(2^(2l+m)l!(m+l)!)x^(2l+m),

(42)

where the factorials can be generalized to gamma functions for nonintegral m. The above equation then becomes

y=a_02^mm!J_m(x)=a_0^'J_m(x).

(43)

Returning to equation (◇) and examining the case k=-m,

a_1(1-2m)+sum_(n=2)^infty[a_nn(n-2m)+a_(n-2)]x^(n-m)=0.

(44)

However, the sign of m is arbitrary, so the solutions must be the same for +m and -m. We are therefore free to replace -m with -|m|, so

a_1(1+2|m|)+sum_(n=2)^infty[a_nn(n+2|m|)+a_(n-2)]x^(|m|+n)=0,

(45)

and we obtain the same solutions as before, but with m replaced by |m|.

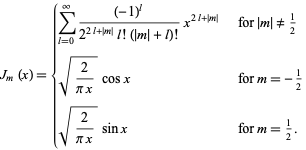J_m(x)={sum_(l=0)^(infty)((-1)^l)/(2^(2l+|m|)l!(|m|+l)!)x^(2l+|m|) for |m|!=1/2; sqrt(2/(pix))cosx for m=-1/2; sqrt(2/(pix))sinx for m=1/2.

(46)

We can relate J_m(x) and J_(-m)(x) (when m is an integer) by writing

J_(-m)(x)=sum_(l=0)^infty((-1)^l)/(2^(2l-m)l!(l-m)!)x^(2l-m).

(47)

Now let l=l^'+m. Then

But l^'!=infty for l^'=-m,...,-1, so the denominator is infinite and the terms on the left are zero. We therefore have

Note that the Bessel differential equation is second-order, so there must be two linearly independent solutions. We have found both only for |m|=1/2. For a general nonintegral order, the independent solutions are J_m and J_(-m). When m is an integer, the general (real) solution is of the form

Z_m=C_1J_m(x)+C_2Y_m(x),

(52)

where J_m is a Bessel function of the first kind, Y_m (a.k.a. N_m) is the Bessel function of the second kind (a.k.a. Neumann function or Weber function), and C_1 and C_2 are constants. Complex solutions are given by the Hankel functions (a.k.a. Bessel functions of the third kind).

The Bessel functions are orthogonal in [0,a] according to

int_0^aJ_nu(alpha_(num)rho/a)J_nu(alpha_(nun)rho/a)rhodrho=1/2a^2[J_(nu+1)(alpha_(num))]^2delta_(mn),

(53)

where alpha_(num) is the mth zero of Jnu and delta_(mn) is the Kronecker delta (Arfken 1985, p. 592).

Except when 2m is a negative integer,

J_m(z)=(z^(-1/2))/(2^(2m+1/2)i^(m+1/2)Gamma(m+1))M_(0,m)(2iz),

(54)

where Gamma(x) is the gamma function and M_(0,m) is a Whittaker function.

In terms of a confluent hypergeometric function of the first kind, the Bessel function is written

J_nu(z)=((1/2z)^nu)/(Gamma(nu+1))_0F_1(nu+1;-1/4z^2).

(55)

A derivative identity for expressing higher order Bessel functions in terms of J_0(z) is

J_n(z)=i^nT_n(id/(dz))J_0(z),

(56)

where T_n(z) is a Chebyshev polynomial of the first kind. Asymptotic forms for the Bessel functions are

J_m(z) approx 1/(Gamma(m+1))(z/2)^m

(57)

for z<<1 and

J_m(z) approx sqrt(2/(piz))cos(z-(mpi)/2-pi/4)

(58)

for z>>|m^2-1/4| (correcting the condition of Abramowitz and Stegun 1972, p. 364).

A derivative identity is

d/(dx)[x^mJ_m(x)]=x^mJ_(m-1)(x).

(59)

An integral identity is

int_0^uu^'J_0(u^')du^'=uJ_1(u).

(60)

Some sum identities are

sum_(k=-infty)^inftyJ_k(x)=1

(61)

(which follows from the generating function (◇) with t=1),

1=[J_0(x)]^2+2sum_(k=1)^infty[J_k(x)]^2

(62)

(Abramowitz and Stegun 1972, p. 363),

1=J_0(x)+2sum_(k=1)^inftyJ_(2k)(x)

(63)

(Abramowitz and Stegun 1972, p. 361),

0=sum_(k=0)^(2n)(-1)^kJ_k(z)J_(2n-k)(z)+2sum_(k=1)^inftyJ_k(z)J_(2n+k)(z)

(64)

for n>=1 (Abramowitz and Stegun 1972, p. 361),

J_n(2z)=sum_(k=0)^nJ_k(z)J_(n-k)(z)+2sum_(k=1)^infty(-1)^kJ_k(z)J_(n+k)(z)

(65)

(Abramowitz and Stegun 1972, p. 361), and the Jacobi-Anger expansion

e^(izcostheta)=sum_(n=-infty)^inftyi^nJ_n(z)e^(intheta),

(66)

which can also be written

e^(izcostheta)=J_0(z)+2sum_(n=1)^inftyi^nJ_n(z)cos(ntheta).

(67)

The Bessel function addition theorem states

J_n(y+z)=sum_(m=-infty)^inftyJ_m(y)J_(n-m)(z).

(68)

Various integrals can be expressed in terms of Bessel functions

J_n(z)=1/piint_0^picos(zsintheta-ntheta)dtheta,

(69)

which is Bessel's first integral,

for n=1, 2, ...,

J_n(z)=2/pi(z^n)/((2n-1)!!)int_0^(pi/2)sin^(2n)ucos(zcosu)du

(72)

for n=1, 2, ...,

J_n(x)=1/(2pii)int_gammae^((x/2)(z-1/z))z^(-n-1)dz

(73)

for n>-1/2. The Bessel functions are normalized so that

int_0^inftyJ_n(x)dx=1

(74)

for positive integral (and real) n. Integrals involving J_1(x) include

int_0^infty[(J_1(x))/x]^2dx=4/(3pi)

(75)

int_0^infty[(J_1(x))/x]^2xdx=1/2.

(76)

Ratios of Bessel functions of the first kind have continued fraction

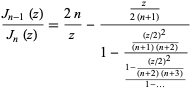(J_(n-1)(z))/(J_n(z))=(2n)/z-(z/(2(n+1)))/(1-(((z/2)^2)/((n+1)(n+2)))/((1-((z/2)^2)/((n+2)(n+3)))/(1-...)))

(77)

(Wall 1948, p. 349).

BesselJ0ReIm BesselJ0Contours

The special case of n=0 gives J_0(z) as the series

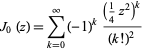J_0(z)=sum_(k=0)^infty(-1)^k((1/4z^2)^k)/((k!)^2)

(78)

(Abramowitz and Stegun 1972, p. 360), or the integral

J_0(z)=1/piint_0^pie^(izcostheta)dtheta.

(79)

Wolfram Web Resources

Mathematica »

The #1 tool for creating Demonstrations and anything technical.

 Wolfram|Alpha »

Explore anything with the first computational knowledge engine.

 Wolfram Demonstrations Project »

Explore thousands of free applications across science, mathematics, engineering, technology, business, art, finance, social sciences, and more.
Computerbasedmath.org »

Join the initiative for modernizing math education.

 Online Integral Calculator »

Solve integrals with Wolfram|Alpha.

 Step-by-step Solutions »

Walk through homework problems step-by-step from beginning to end. Hints help you try the next step on your own.
Wolfram Problem Generator »

Unlimited random practice problems and answers with built-in Step-by-step solutions. Practice online or make a printable study sheet.

 Wolfram Education Portal »

Collection of teaching and learning tools built by Wolfram education experts: dynamic textbook, lesson plans, widgets, interactive Demonstrations, and more.

 Wolfram Language »

Knowledge-based programming for everyone.

Find a General Solution in Terms of Bessel Functions

Source: https://mathworld.wolfram.com/BesselFunctionoftheFirstKind.html